Ch 2: The Law of One Price

There is only one risk-free discount function and its discount factors do not lie

This is the second in my series (An Introduction to Quantitative Finance) which began with a review of present values. To retrieve present values, we need discount rates. There must be some degree of coherence among discount rates across maturities. This coherence is enforced by the law of one price. The law is not a natural law, but we will see how it is enforced by the existence of arbitrage opportunities.

Theoretical zero (aka, spot) rate curve

For this discussion, I'll refer to risk-free interest rates only. In many contexts, the proxy for a risk-free rate is a U.S. Treasury rate or yield. There is fascinating theory (and practice) around the risk-free rate(s), but I'll skip it for now¹. We do naively assume there exists a theoretical spot rate curve: a plot of risk-free spot (aka, zero) rates for each maturity. I tend to textually represent this curve as a vector at six-month intervals; e.g., the 2-year zero-rate curve can be given by {0.015% @ 0.5 years, 0.058% @ 1.0 year, 0.100% @ 1.5 years, 0.148% @ 2.0 years} which in context simplifies to the short vector: {0.015%, 0.058%, 0.100%, 0.148%}.

There is a drawback to my zero rate vector, can you spot it (pun intended)? Strictly, they are incomplete specifications unless we know to assume the compound frequency is semi-annual (it is reasonable to assume the compound frequency matches the interval, but it is not necessary). Take the above 1.5-year rate of 0.10%; that’s 0.10% per annum with semi-annual compound frequency. We should realize that 0.10% specified with annual compound frequency is a slightly lower actual rate; and 0.10% specified with monthly or continuous frequency are each slightly higher actual rates. This is so fundamentally important that I will repeat with an example:

“An 8.0% per annum interest rate” or
“An 8.0% interest rate”

The above statements are functionally equivalent because the stated (aka, nominal) rate is annualized—i.e., given in per annum terms—by strong and useful convention. So there is nothing wrong with either statement except each is incomplete. We are missing the rate’s periodicity; aka, compound frequency. This can lead to calculation errors. If the periodicity is monthly, then the equivalent annual rate is (1 + 0.080/12)^12 - 1 = 8.30%. If the periodicity is continuous, the equivalent annual rate is exp(0.080) - 1 = 8.329%. Each of these rates is literally a different rate, hence the superiority of discount factors.

Discount factors do not lie

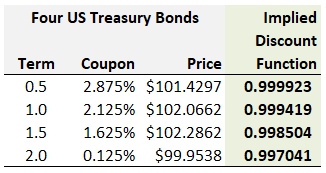
It is more efficient to represent the zero-rate curve as a discount function; a discount function is a vector of discount factors. I will use a simplified fragment of Bruce Tuckman's example². See below.

The first three columns assume three riskfree (U.S. government) coupon-bearing bonds and their observed prices. We assume the observed prices as inputs in order to bootstrap the zero rate curve. We start from the shortest bond. A natural way to solve for the six-month and one-year zero rates³ is the following:

$101.4297*(1 + z6)/2) = $101.4375,
z6 = (101.4375/101.4297 - 1)*2 = 0.015%.

$1.06250/(1 + 0.015%/2) + $101.06250/(1 + z12/2)^2 = $102.0662,
z12 = [sqrt(101.06250/[102.0662 - $1.06250/(1 + 0.015%/2)]) - 1]*2 = 0.58%

First we solved for the six-month rate of 0.015%, then we used it to infer (aka, bootstrap) the one-year rate.

The above is a common approach for CFA/FRM exam-type questions. But it is better to apply the discount factors directly, as follows:

$101.4297 = $101.4375*d6,
d6 = 101.4297/101.4375 = 0.999923

$1.06250*d6 + $101.06250*d12 = $102.0662,
d12 = $1.06250*d6 + $101.06250*d12 = [102.0662 - 1.06250*d6 ] / 101.06250 = 0.999419

We expect an upward slope, which this (Tuckman's) example does exhibit. Just as the zero rates are increasing with maturity, the corresponding discount factors are decreasing with maturity. A natural discount function is a vector of decreasing discount factors to reflect the decreasing value of a $1.00 received sequentially further in the future. Each discount factor itself is today’s value of $1.00 in the future.

GARP's Flawed (Mock Exam) Question Illustrates

I am a public critic of GARP's FRM questions because the association writes far too many questions that are imprecise, careless, or even just wrong⁴. Consider the following mock exam question written by GARP⁵ :

There is a stated solution that pretends to depend on the law of one price, but in fact the seemingly simple scenario is incoherent. 

• According to the first bond, the 1-year discount factor is given by d12 = $98.44/$102.8750 = 0.95650; with an implied semi-annual spot rate of [sqrt(1/0.95650)-1]*2 = 4.497%.

• According to the third bond, the 1-year discount factor is given by d12 = $101.30/$106.250 = 0.95341; with an implied semi-annual spot rate of [sqrt(1/0.95341)-1]*2 = 4.828%.

Consequently, this question violates the law and, in fact, has no solution. In a frictionless world, how would we exploit this situation? We sell the expensive thing and buy the cheap thing. Specifically,

• We immediately short (aka, sell) 100.0% face amount of the 2.875s which generates $98.40 in cash

• We immediately buy (aka, long) 96.82% face amount of the 6.250s which costs us 0.968235 * $101.30 = $98.08.

• The difference is today's profit: $98.40 - 98.08 = $0.23. In one year, the long bond returns 96.82% * $106.25 = $102.8750 which is exactly what will owe on our short position. There are no future cash flows; the initial +$0.23 is a riskless profit. Our trade is an arbitrage that exploits the violation of the law of one price. Our trade itself nudges each bond’s price, as if the law were as a gravitational force pulling the prices toward the law’s requirement: there cannot be two different one-year discount factors, there can be only one!

Recall my initial condition was the presumption of riskfree rates. If these bonds are without risk, the initial profit ($0.23) is riskless because my offsetting future long/short payoffs are assured!

The natural sciences have laws (e.g., Newton's, gravitation) that find elegant mathematical descriptions. Finance is a social science without such laws. This “law” of one price theoretically enforces a single discount function—and in turn—the practical ability of arbitrageurs to trade is what enforces the discount function.

The law of one price says there is only one riskfree discount function; and this function is cleaved to a single set of spot rates, forward rates, and par yields, too.

Here is Tuckman's definition of the law of one price: 

"Absent confounding factors (e.g., liquidity, financing, taxes, credit risk), identical cash flows should sell for the same price.” — Tuckman, Bruce

Here's my definition: 

The law of one price says there can be only one riskfree discount function (aka, set of discount factors) at any moment in time, absent confounding factors. 

Of course the discount function allows us to translate into implied spot rates, forward rates and par yields. It is not really a translation: they are alternative expressions of the same theoretical zero rate curve. At the risk-free rate level, there is only one spot/forward/par rate curve. Let's continue with Tuckman's example of {0.9999230, 0.9994190, 0.9985040, 0.9970410} and using the 2-year discount factor (i.e., 0.9970410) to illustrate:

• The 2-year spot rate is given by, S(2.0) =  [(1/dt)^(1/2t) - 1]*2 = [(1/0.9970410)^(1/4) - 1]*2 = 0.148%

• The six-month forward rate starting in 1.5 years is given by F(1.5, 0.5) or F(1.5, 2.0) = (d18/d24 - 1)*2 = (0.9985040/0.9970410 - 1)*2 = 0.293% (rounded) or 0.294% (more accurate)

• The 2-year par yield is given by (1-d24)/(d6 + d12 + d18 + d24)*2 = (1-0.9970410)/3.9948870*2 = 0.148%. Imperceptibly lower than the spot rate, but note the elegant expression! Below the rounded par yields match the spot rates because they are only slightly lower throughout, but they are actually different values.

Here is an updated table. Again, we can refer to spot rates, or forward rates, or even par yields, but they are but different faces of the same single discount function. Many faces, one truth (absent confounding factors).

Why the discount factors do not lie

This brings me to the advantage of the discount factors over spot rates and the meaning of the phrase discount factors do not lie⁶. Unlike spot rates, discount factors do not require us to specify a compound frequency! Consider our two-year discount factor, d24 = 0.9970410. We already found above that is corresponds to a (less rounded) spot rate of 0.14822% per annum with semi-annual compound frequency. If we apply the same formula, we can retrieve various two-years spot rates; each of these are different stated (aka, nominal) rates but they are identical actual rates:

• 0.14818% per annum with monthly compound frequency

• 0.14828% per annum with annual compound frequency; aka, effective annual rate

• 0.14817% per annum with continuous compound frequency

You could say the discount factors embed the compound frequency—and I’ve written that on our forum—but I think it’s more accurate to say discount factors are cheerfully oblivious to compound frequencies. The simpler truth here is that the present value of $1.00 riskless dollar received in two years is $0.997041. It is subtle but notice how easy it is to misperceive that the values above; i.e., 0.14818%, 0.14828%, and 0.14817%; are different rates when actually they are not different rates. Conversely, the same literal 0.14818% does translate into different rates under different compound frequencies.

Actual bonds trade rich or trade cheap because other factors do confound

The zero rate curve--as described by the discount function--is a theoretical curve. Using it to price a bond generates a theoretical or model price. For example, given our discount function, what is the theoretical price of 2-year (remaining) Treasury bond that pays a 8.0% semi-annual coupon? 

We expect its price to be $117.68 because the sum of the its discounted cash flows is given by $4.00*0.9999230 + $4.00*0.9994190 + $4.00*0.9985040 + $104.00*0.9970410 =$117.68.⁷

But the "confounding factors" are never absent: the actual observed (aka, traded) price will likely be a bit higher or lower. We both expect the price to be $117.68 and also expect it to be different. If we observe the price to be $117.85, we can say the bond is trading rich; if we observe the price to be $117.39, we can say the bond is trading cheap. Trading rich and cheap are realities, just as reality includes the frictions that confound the law’s pristine assumption (arbitrageurs do not have the benefit of frictionless trading).

---

Thank you for reading. I hope you found this to be a helpful primer. I also hope it convinced you that discount factors (and the discount function) are a robust way to characterize the riskfree interest rate curve. See you next time.

P.S. I did NOT use any AI to write this article; i.e., AI contributed exactly zero (0%) to this text. Although I increasingly do utilize my GPT-4 paid subscription for many purposes—and I actively look for more use cases—I’ve yet to allow GPT-4 to write text for me. I don’t need it for this basic concept, and I prefer to practice the craft of writing. Everything is practice, especially this. My current view is that GPT-4 is overrated for generative text-writing but underrated for meta-creative use cases.

I did however use MidJourney for the social image cover: I think it’s an okay (not great) image, my MJ skills have a long way to go but I’m learning from super-helpful Heather Cooper and these guides, too.

1. Identifying the risk-free rate is nontrivial. LIBOR was just phased out, but LIBOR was always an unsecured rate with credit risk, in addition to being hypothetical. The new reference rates (e.g., SOFR, ESTER, SONIA) are better (being secured) but they are backward, overnight rates. Of course, U.S. Treasuries are academically common but these rates are artificially depressed by tax and regulatory factors; not to mention last week’s downgrade by Fitch.

2. Tuckman, Bruce; Serrat, Angel. Fixed Income Securities: Tools for Today's Markets (Wiley Finance) (p. 54). Wiley. Kindle Edition. Chapter 1. Tables 1.2, 1.3 and 1.4. This is also the source of the subsequent quote by Bruce Tuckman.

3. To write cleaner notation, I’m using z6 for the six-month zero rate which is typically denoted by s(0.5); similarly, the z12 refers to the one-year zero rate, s(1.0). Similarly, d6 refers the six-month discount factor, d(0.5), and d12 refers to the one-year discount factor, d(1.0).

4. My criticism is a wholly justified appeal to threshold quality in light of a large, evidentiary fact pattern. The exam is an expensive and time-consuming adventure for customers. Our large-sample analysis provides statistical evidence of a meaningful error-imprecision rate (i.e., probably ~30% but at least 20% with high confidence). See my long memo—filled with concrete examples—here at https://forum.bionicturtle.com/threads/how-to-fix-the-frm-davids-2018-memo-to-the-frm-committee-and-garps-board-of-trustees.22758/

5. 2010 Practice Exam, Part 1, Question #18, page 38; GARP, Global Association of Risk Professionals, Inc., 2010.

6. This is a phrase that I personally first encountered a long time ago (maybe two decades?) on Paul Wilmott’s forum

7. Careful readers may notice that I added a zero to the end of the discount factors: 0.9999230, 0.9994190, etc. Out of habit, I’ll often add the zero so that 0.99923 isn’t misunderstood as a rounded number. Under the coupon column, I might have done that (i.e., I might have represented 2.875% as 2.8750%) except we sort of know those are in 1/8th increments.